Skip to main content

数据结构和算法学习笔记

· 11 min read
LIU

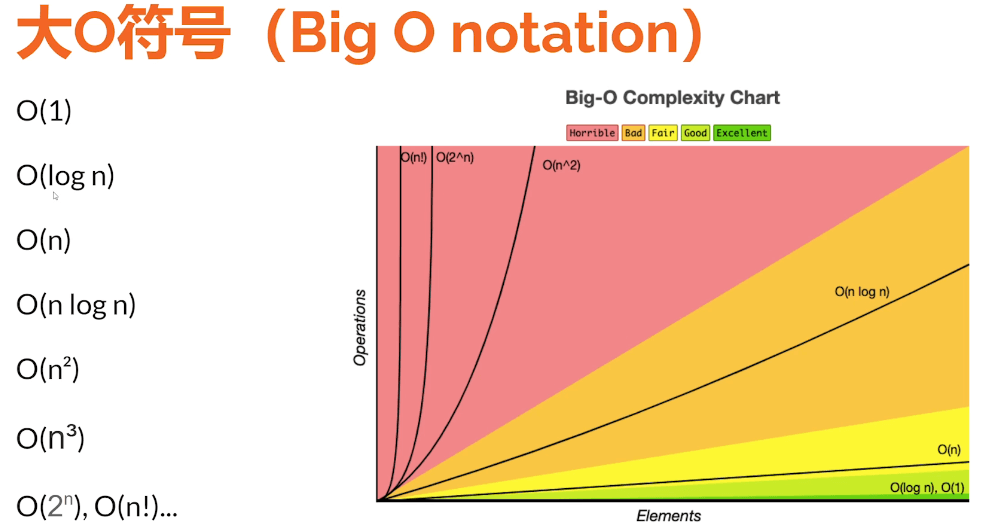
时间复杂度​

一般看的都是 O(1) ~ O(n^2) 范围，其它都是需要优化的

  • O(1)

    • if(i==1)
    • res = 100 1000、res = n 200
    • push(2)、pop()
    • map.set(1,1)、map.get(1)
    • 计算复杂度时，O(1)一般会被忽略

  • O(n)

    • for循环，while循环（不使用二分搜索）

  • O(log n)

    • 二分搜索

  • O(n log n)

    • 排序，编程语言自带的排序方法
    • sort()

  • 复杂度的计算

    • 取复杂度最高的一项作为总体复杂度，前面的常数忽略
    • n^3 + n^2 +1 时间复杂度是 n^3
    • 2n^2 + 3n + 6 时间复杂度是n^2

  • 优化的方法：从低一级的复杂度寻找灵感

    • O(n) -> O(log n) 使用二分搜索
    • O(n log n) -> O(n) 遇到需要排序的题,想想能否通过数组,set, map,heap解
    • O(n^2) -> O(n log n)遇到嵌套循环,想想能不能通过排序+一个for循环解

空间复杂度​

  • O(1)
    • 与时间复杂度不同，有很多题的空间复杂度就是O(1)
    • const a = 1
    • let a = 'dd'
  • O(n)
    • 定义一个长度为n的数组
    • 定义一个长度为n的set，map
    • 用for循环生成一个长度为n的链表
  • O(n^2)
    • 二维数组
    • 一维数组每个元素存放一个长度为n的set或者map或者链表

image-090642534

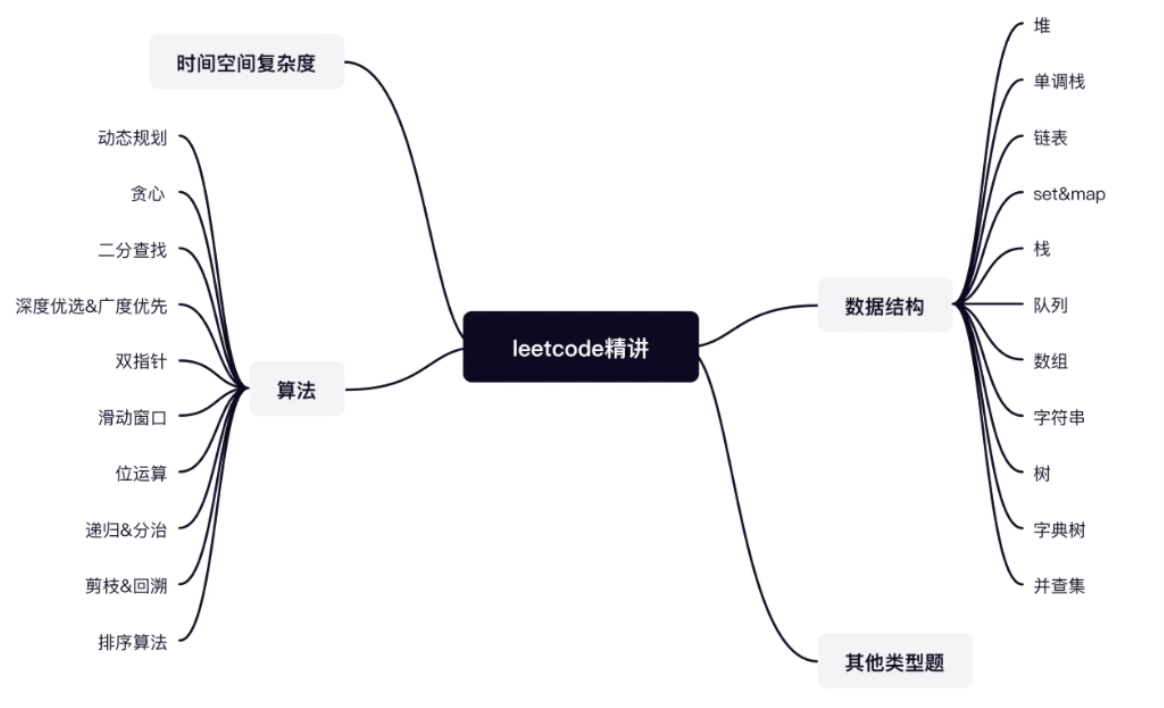
image-20220501131654895

栈​

  • stack
  • 栈是一个后进先出的数据结构
  • JavaScript 中没有栈，但是可以用Array数组实现栈的功能
  • 常用操作包括：push 、pop 、stack[stack.length-1]
  • stack 、callStack
  • 栈顶 = 数组的最后一位

使用场景：十进制转二进制、判断字符串的括号是否有效、函数调用栈

let stack = []
stack.push(1)       // [1]
stack.push(2)       // [1,2]
stack.push(3)       // [1,2,3]
stack.pop()         // [1,2]
stack.pop()         // [1]

队列​

  • queue
  • 队列是一个先进先出的数据结构
  • JavaScript 中没有栈，但是可以用Array实现队列的功能
  • 常用操作包括：push 、shift、queue[0]
  • 先进先出，保证有序性

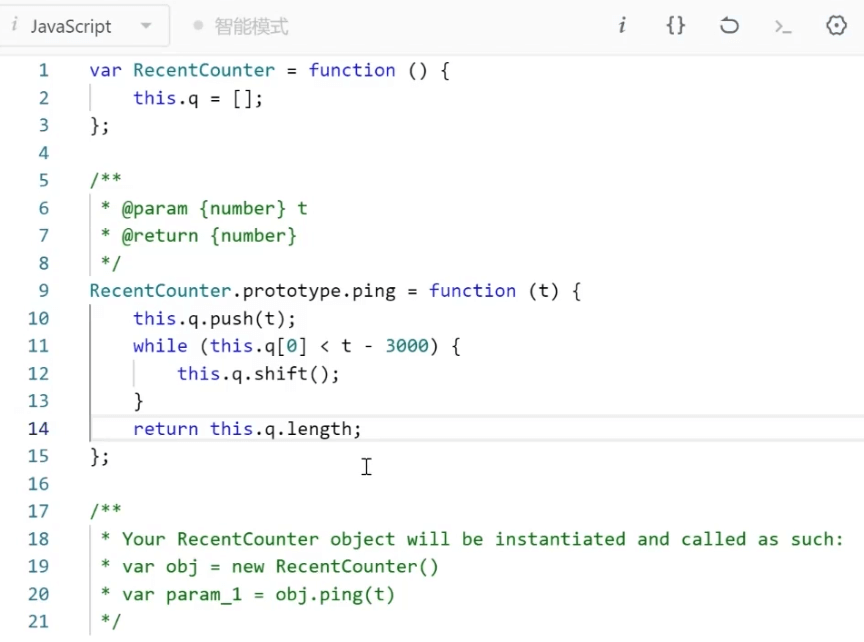
使用场景：食堂排队打饭、js异步请求中的任务队列、计算最近请求次数

let queue = [] 
queue.push(1)       // [1]
queue.push(2)       // [1,2]
queue.push(3)       // [1,2,3]
queue.shift()       // [2,3]
queue.shift()       // [3]

  • js是单线程的，无法同时处理异步中的并发任务

  • 使用任务队列先后处理异步任务

image-114250056

计算最近请求次数：leetcode 933

image-1105321185

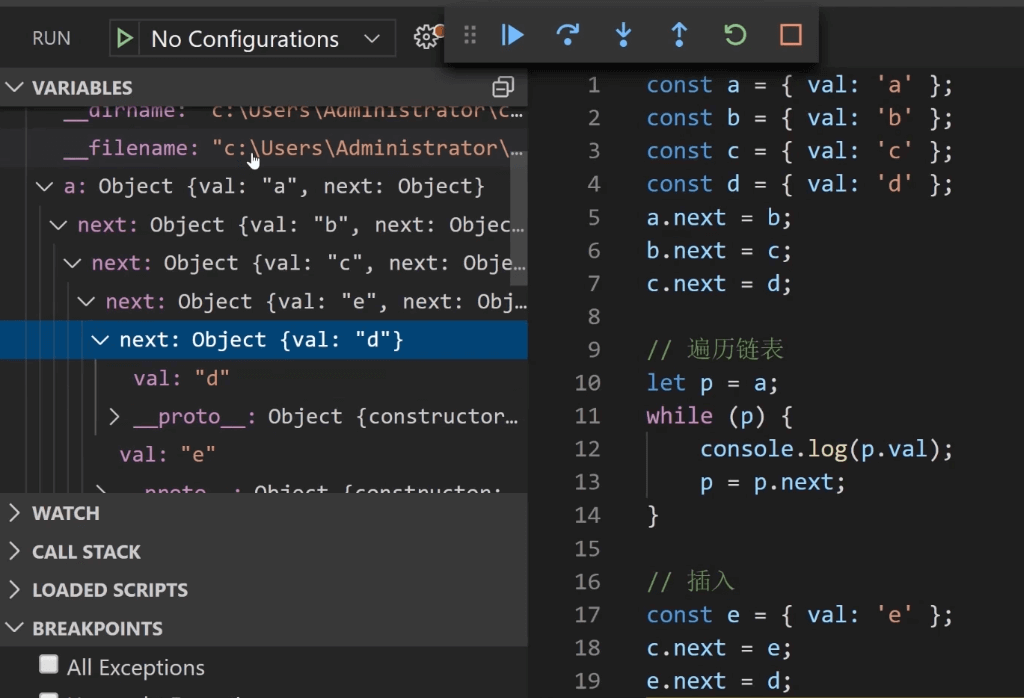
链表​

  • linkedList
  • 多个元素组成的列表
  • 元素存储不是连续的，用next指针连在一起
  • JavaScript中没有链表，用Object模拟链表
  • 链表常用操作：修改next、遍历链表、指针
  • JS中的原型链也是一个链表
  • 使用链表指针可以获取JSON的节点值

image-114608450

链表 vs 数组​

  • 数组：增删非首位元素时往往需要移动元素
    • 访问速度极快
    • 有顺序
    • 访问复杂度是O1
    • 新增和删除复杂度是On
  • 链表：增删非首位元素，不需要移动元素，只需要更改next的指向即可
    • 不能随机访问
    • 新增和删除复杂度是O1

image-121741790

删除：

c.next = d

LeetCode: 237．删除链表中的节点​

⑨ -- ① -- ③ -- ②

解题步骤：

  • 将被删节点的值改为下个节点的值
  • 删除下个节点
var deletNode = function (node){
        node.val = node.next.val
    node.next = node.next.next
}

时间和空间复杂度都是 O(1)

LeetCode: 206.反转链表​

前端与链表：JS中的原型链​

  • 原型链的本质是链表

  • 原型链上的节点是各种原型对象，比如

    • Function.prototype 、Object.propotype ......

  • 原型链通过__proto__属性连接各种原型对象

  • 如果A沿着原型链能找到B.prototype,那么A instanceof

实现instanceof

function ins(a,b){
    //指针
  let i = a
  while(i){
    if(i===b.prototype) return true
    //这里修改的是上面赋值的变量，不会改变实参 a
    i=i.__proto__
  }
    return false 
}

集合​

  • 一种无序且唯一的数据结构
  • ES6中有集合，是 Set
  • 常用操作：去重、判断某元素是否在集合中、求交集差集
//去重
const arr = [1,2,2,3]
const a = [...new Set(arr)]

//是否存在
const set = new Set(arr);
const has = set.has(3)

//求交集
const set2 = new Set([2,3])
const set3 = new Set(arr.filter(item=>set2.has(item)))
//差集
const set3 = new Set(arr.filter(item=>!set2.has(item)))

字典​

  • 与集合类似，字典也是一种存储唯一值的数据结构，但它是以键值对的形式来存储
  • ES6 中有字典，是 Map
  • 字典的常用操作：键值对的增删改查
const m = new Map();
//增
m.set('a','aa');
m.set('b','bb');

//删
m.delete('b');
m.clear()

//改
m.set('a','aaaa')

//查
m.get('a')

//以上时间复杂度都是O(1)

树​

  • 一种分层数据的抽象模型
  • 前端：DOM、树、级联选择、树形控件
  • JS中没有树，但是可以用 Object、Array 构建树
  • 树的常用操作：深度/广度 优先遍历、先中后序遍历

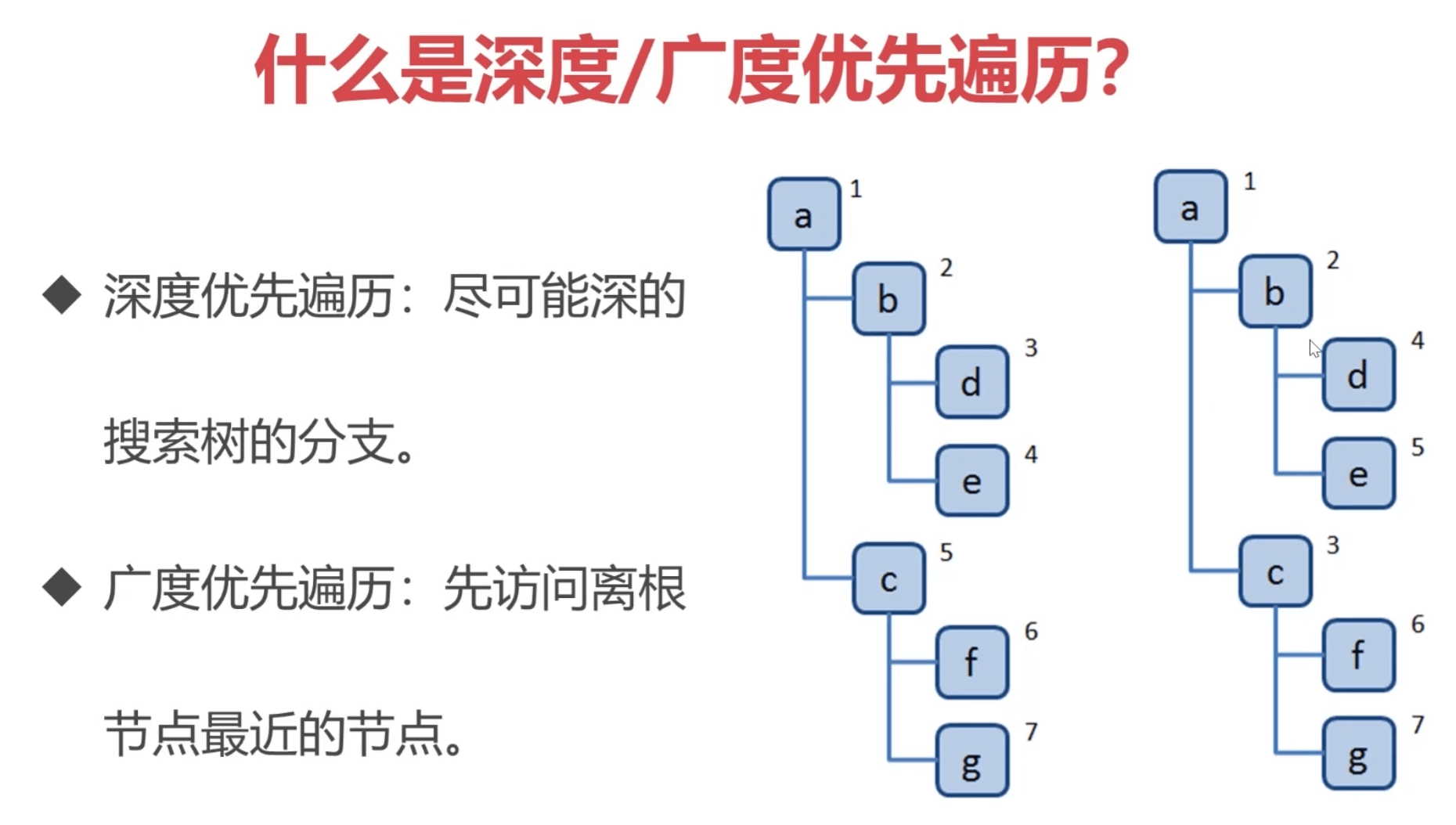
image-094847488

//广度
function g(root){
  let queue = [root];
  while(queue.length>0){
     let cur = queue.shift()
     cur.children.forEach(item=>{
        queue.push(item)
     })
  }
}

二叉树​

  • val、left、right
//反转二叉树
var invertTree = function(root) {
    if(root==null)return root; //js如果if一行缩写return，一定要加 ; 在最后
    [root.left,root.right] = [invertTree(root.right),invertTree(root.left)]
    return root
};

图​

前端用的场景较少

例如：Vite和webpack里面每个module的依赖关系、moudleGarph 内部文件依赖图

堆​

  • JS中通常用数组表示堆

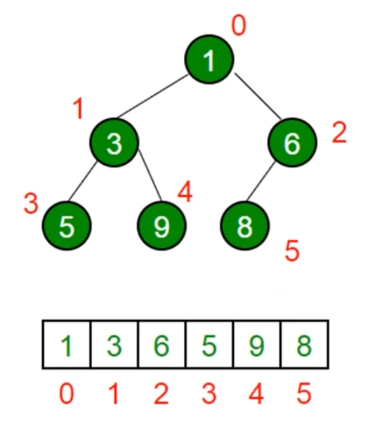
image-214746136

  • 左侧子节点的位置是 2 * index + 1
  • 右侧子节点的位置是 2 * index + 2
  • 父节点位置是 （ index - 1）/ 2
  • 堆 能高效、快速地找出最大值和最小值，时间复杂度：O(1)
  • 找出第K个最大（小）元素

排序和搜索​

  • JS中的排序：数组的 sort 方法
  • JS中的搜索：数组的 indexOf 方法

冒泡排序​

是最简单，但性能不好

回溯算法​

回溯法也可以叫做回溯搜索法，它是一种搜索的方式

回溯和递归是相辅相成的，只要有递归就会有回溯

递归函数的下面，就是回溯的逻辑

二叉树在递归的过程中，有些也会用到回溯

回溯：纯暴力的搜索，并不是一个高效的算法，因为有些问题能用暴力解出来已经很不错了，用for循环一层一层嵌套也根本搜不出来

  • 切割问题（如字符串）、子集问题、排列问题 （强调元素的顺序）、组合问题（不强调元素的顺序）、棋盘问题

  • 是一种渐进式寻找并构建问题解决方式的策略

  • 会先从一个可能的动作开始解决问题，如果不行，就回溯并选择另一个动作，直到将问题解决

  • 有很多路，很多组合

  • 这里路里，有死路，也有出路

  • 通常需要递归来模拟所有的路

  • 全排列

    • 用递归模拟出所有情况
    • 遇到包含重复元素的情况，就回溯
    • 收集所有到达递归终点的情况，并返回

  • 回溯法通常都可以抽象为一个n叉树

贪心​

每一步都选择当前最优解，跟之前的选择没关系

例 找零钱

贪心无套路

动态规划​

求极值

每一步的状态，是前一步推导而来

步骤：

  1. 确定dp数组 （dp table）以及下标的含义
  2. 确定递推公式
  3. dp数组如何初始化
  4. 确定遍历顺序
  5. 举例推导dp数组

记​

动态规划是由前一个状态推导出来的，而贪心是局部直接选着最优的